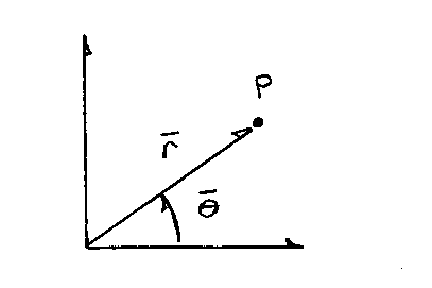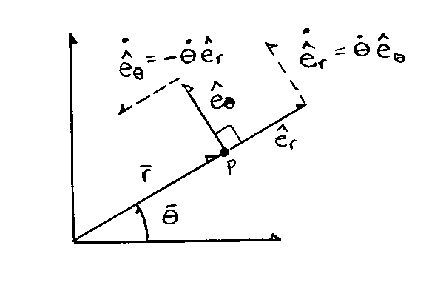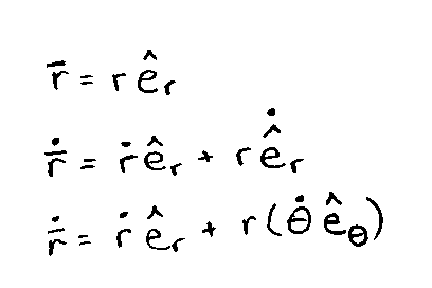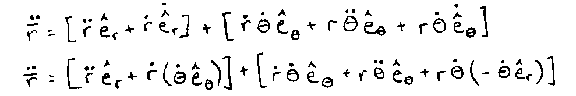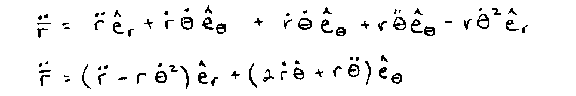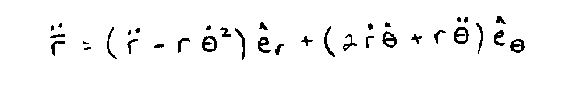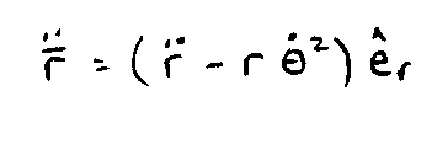Math & Physics


	VECTOR CALCULUS Deriving radial & tangential acceleration

	I don't like mathematical proofs; I'm just not particularly good at them. I'm a little better at derivations, but not by much. However, this is one derivation that I do like, so I'll work through it here as my favorite vector calculus derivation. Like most math and physics problems, they can be solved in a variety of ways, so this is only one approach. It happens to be the approach I think is most fundamental, however. I am going to work through this problem the way I wish these problems were presented during school, so this is my method and it is the way I would teach the problem. What is my method? The primary element is that I create the organized spaces in my brain before I try to fill them up with numbers.

1.	Q: What are we about to do?	A: We are going to develop a general expression for radial and tangential acceleration. However, we will only consider radial acceleration.

2.	Result: a_r = v² / r	This will be the end result of our efforts. It's the answer.
	What does the equation mean? This is the acceleration felt as your body gets "pushed" while seated in a turning vehicle. It is radial acceleration.

3.	Relevance	Why should you care?
	In this particular case, I was at work in Afghanistan when a former Marine asked me about flying the F-15. The conversation got into how many g's the F-15 can pull and how tight the turn radius was. I explained the turn radius depends only on speed and g-loading; it's a simple mathematical relationship where the g-loading equals the velocity squared divided by the radius. Here's the physics formula: a = v²/r G-loading is how many times the force of gravity can be felt while in a turn, so that "a" is the g-loading times the force of gravity. Since an F-15 can pull 9 g's at 440kts, it's a matter of solving for "r" and making a few unit conversions: r = v²/a Use dimensional analysis to convert 440 kts into ft/s: 440 kts = (440 nm / hr)(1 hr / 3600 s)(6076 ft / nm) = 746 ft/s Acceleration is g-load times force of gravity: *a = 9 32 ft/s² Solve the equation: r = (746 ft/s)² / (9)(32 ft/s²) = ~1900 ft** Sanity check: This answer is about right. The tightest an F-15 can turn is more like 2500 - 3000 ft because that 1900 ft is an instantaneous capability. At 9 g's, the airspeed rapidly decays and the g-loading falls off, so 2500 - 3000 ft over 180 - 270 degrees of turn is more realistic, but the math is accurate for that snapshot in time.	The tighter the turn, the harder it is for an enemy aircraft to get into a position of advantage to point the guns and missiles and vice versa. 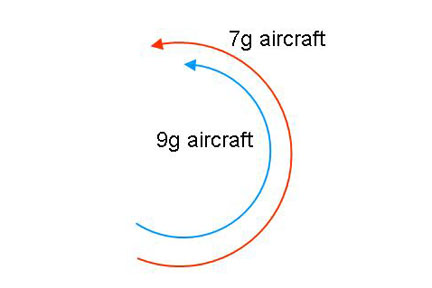All the stuff that can kill an adversary comes off the front of a jet fighter: missiles and bullets. If you can keep your nose on the other aircraft (or keep the enemy's nose off), then you can win the engagement. A higher g aircraft can turn tighter and outmaneuver an opponent. I had one opportunity to fly against F-14 Tomcats during a Roving Sands mission. I'm used to training against fellow F-15 or F-16 aircraft, which are 9g capable jets. The F-14 is about a 7g aircraft. When I first saw the F-14s, I was in a position of advantage up high and I rolled in to attack. There were three of them, and the first thing that struck me was how big they were... and this is coming from an F-15 driver! The Tomcats immediately threw out their wings and started a defensive turn. To be honest, I wondered what they were doing at first because they just couldn't turn tight enough to prevent my attack. I just dialed up 9g's, and starting at the back of their pack I just drilled each one with a gun shot as they quacked. To be fair, the F-14 is a third generation fighter (vs 4th), and it is meant for fleet defense, so it's not a contest. It does, however, make a nice movie prop.
4.	Coordinate System	Always draw a coordinate system for a physics problem!
	Several coordinate systems are available, so it's really a matter of choosing the most convenient system to describe the problem. We are most familiar with the Cartesian system, but curvilinear (polar) coordinates are a close second for describing rotational or curvilinear motions
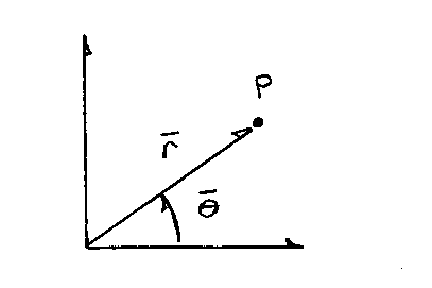		I did draw the typical x-y axes, but just for reference. It's the r and theta which count. We're only working in two dimensions since it's a flat page and I'm not trying to describe another dimension of movement. It only takes two coordinates to fully describe any place our particle "P" can be, so this is a two-degree of freedom (2-DOF) system. Although I could choose whatever direction I want for positive movement, the only thing that matters is consistency. I've chosen theta as increasingly positive in the ccw direction and r is positive as it moves away from the origin. I mentioned that I think the vector calculus version (my version!) is the best derivation. The biggest reason is no conversion from Cartesian to polar is required. I mean seriously... if we chose to work a problem in polar coordinates and then have to fumble around with a Cartesian to polar conversion (using sine and cosine), what is the point? Google it. Most derivations use sine and cosine when they profess to be a polar coordinate system derivation. Why not just throw in an elliptical coordinate conversion while they're at it?
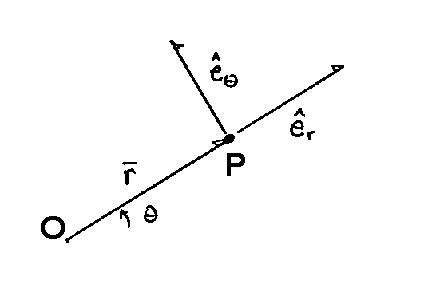		r and theta are the vectors to identify point P and consist of both magnitude and direction. Several conventions exist for writing the unit vectors for curvilinear systems, but I'll use e-sub-r and e-sub-theta as drawn. These are the "unit" vectors since they always have a length of one. It's easiest to draw them from point P. They are always perpendicular to each other. e-sub-r is always aligned outward from the origin and e-sub-theta is always oriented in the direction of angle theta. The vector r is properly written as (using bold to indicate a vector): r = re_r That's it. However, it begs the question as to why there is no theta component. I still don't have a perfect answer for this, but the angle has no point of reference since there is no "x-axis" to start from; it only indicates a positive movement direction. The position vector r starts at zero from the origin, but there is no "zero" for theta.
5.	Vector Basis Moves	Every motion (position, velocity, acceleration) can be expressed in the originally described coordinate system!
	If those unit vectors move, they move "incrementally" in orthogonal directions. As point P moves around, the position vector r stays fixed at one end to the origin and the e-dot velocities of those unit vectors move in some direction of the original coordinate system; it's just a matter or rewriting those unit vector velocities back into the coordinate system. This part is the key to all of vector calculus! This is the difficult part and everything else is just calculus.	How fundamental is the above statement? It's fundamental enough to get written in bold. If we said this was a 2-DOF system using only two coordinates to fully describe the motion, then no matter what happens, we should still be able to write the equation in the same two coordinates.
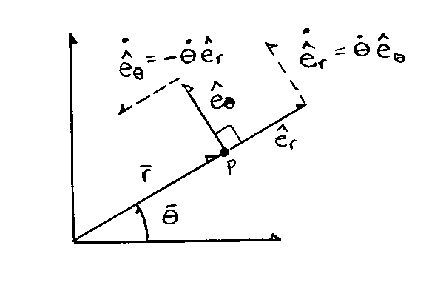		e-sub-r is a unit vector, and if it moves (as point P moves), it has a velocity of e-dot-r in the e-sub-theta direction. Therefore, e-dot-r can be rewritten as an angular velocity magnitude of theta-dot in the e-sub-theta direction. e-sub-theta also moves, and in that very infinitesimal manner, e-dot-theta moves in the negative e-sub-r direction with a velocity of theta-dot. Getting this part correct is key to the entire process. These are not big moves, but as with calculus in general, they are infinitesimal moves and can be pictured to make those slight movements in the original coordinate system. Now it's just a matter of using the product rule over and over again to get the solution we're after.

6.	The Derivation
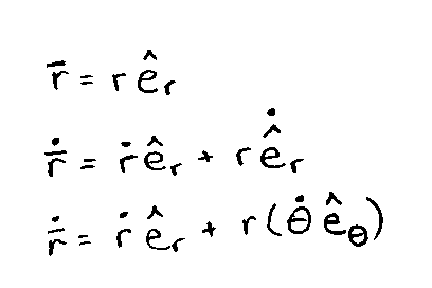		Start with the position vector. Take the first time derivative of position, using the product rule for each multiplier: the derivative of r times e-sub-r plus r times the derivative of e-sub-r. It's standard product rule and those unit vectors count in the process! Now, we can't do much with that e-dot-r term, so rewrite it back into the original coordinate system as discussed above. This is velocity in polar coordinates.
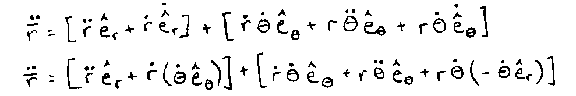		Take the second time derivative to get acceleration. It's just a matter of the product rule again. Velocity had two terms and each of those terms appear in the brackets. The first velocity term had two multipliers, so each one of those gets their own term from the product rule of calculus. The three multipliers result in a three term set in the second brackets. Rewrite the pesky e-dot-r and e-dot-theta terms back into the original coordinate system as discussed in Section 5 above.
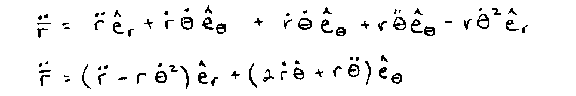		Just gather up the terms and we have the general form of acceleration in polar coordinates. All that remains is to make sense of the result based on the goal we started with.

7.	The Result
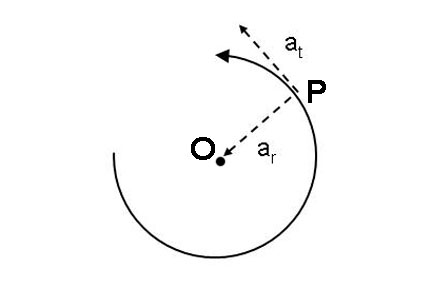
	Here's the coordinate system we set up:	Here's the same coordinate system, written for a particle P moving in a circular path with both tangential and radial acceleration as depicted. It's the same thing as written to the left.

	Looking at the generalized result of the derivation, we have both components, radial, e-sub-r and tangential, e-sub-theta:

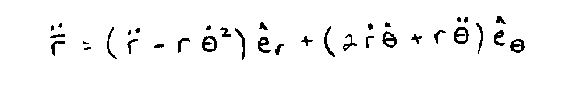	Let's look at only the radial component since that's where we started and we're interested in that acceleration we feel pushing us in our turning vehicle, or the g's felt by a maneuvering F-15:
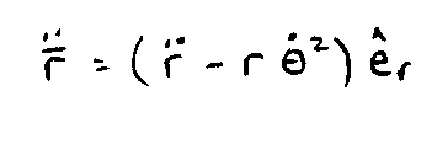		This is a vector component in the e-sub-r direction; radial acceleration, so we know the direction. The magnitude of this acceleration is in the parentheses. The first term, r-dot-dot, is simply the acceleration of the particle P if it was moving straight away from the origin in a straight line; no turning. If we are holding a constant radius turn, then we're not moving in the r direction, so r-dot-dot is zero. This leaves us with only the second term, minus r theta-dot-squared.

7.	Relationships
	There are a lot of notation conventions and other standard relationships to help get the result into the form we want. Here's where we are:
	r-dot-dot = (-r)(theta-dot)²	This is the above equation, acceleration in the radial direction when the radius of turn is constant.
	r-dot-dot = a	r-double-dot is the second time derivative of r, which is just acceleration. Technically, it should be a_r since we're only considering that radial term.
	theta-dot = ω	Just another convention. They are exactly the same.
	Now we have the following form:
	a = -rω²
	Close! We're very close! Actually, we could stop right here, but the problem is that omega term. If I want to describe how fast a CD is spinning, then angular velocity, omega, is perfect. However, we don't drive or fly in terms of angular velocity, so having it written in this form is not very helpful. We drive or fly with "instantaneous" forward speed. It's always a forward speed and it's only due to forces acting on our motion that our straight line speed keeps changing direction into this circular path. What we need is tangential velocity, not radial (angular) velocity. Lucky for us, we already solved it above! Go back up to Section 6, line three and we have the first time derivative for position r, which is velocity. It has both radial and tangential terms, just like our acceleration equation. Let's pick out the part we need, the tangential component, and we have:
	r-dot = (r)(theta-dot)(e-sub-theta)	From Section 6 above
	r-dot = (r)(theta-dot)	Get rid of the e-sub-theta because we know we only want this tangential term.
	v = rω	Just some notation substitutions: r-dot = v theta-dot = ω
	Make the final substitution since ω = v/r:
	a = -rω²
	a = -r(v/r)²

8.	The Result

	a = -v² / r	The final result we wanted from the beginning!
	The only difference is the negative sign, and this is technically correct. When we set up the coordinate system in Section 4, the e-sub-r vector pointed away from the center of the circle. The negative sign means the acceleration is pointed toward the center of the circle, opposite of the convention we set up. This means some force is acting on our car (friction of turning wheels) or aircraft (lift) that is accelerating the vehicle toward the center of the turn circle and our bodies are constantly getting pushed by the vehicle toward the center. This is why we "think we feel a force" pushing us away, like we want to get thrown off the merry-go-round. The acceleration is inward, but we feel the force of the solid vehicle pushing us in the direction of this acceleration.
	This is the "tool" to solve our physics problems. Everything we did to get here was just to build this tool. Rarely are we asked to build our own tools like we did here; we just need to know which ones to use to solve our problems. If I need a hammer to build a shed, I just go to the tool store and buy a hammer. I don't melt a bunch of metal and make my own hammer; someone else has already done that hard work like all of the above steps. So, knowing the above formula, I can easily answer the question about how tight an F-15 can turn based on speed and g, just like when we started.
	Why bother with the derivation in the first place? Mathematicians, scientists, engineers and good students don't like mysteries unless they're watching a movie! By working through it at least once, we can understand where it comes from logically. In a more esoteric sense, if we ever do get stuck, or if we want to use our tools like a master craftsman, then knowing where they came from can be helpful.

9.	Application
	To finish this off properly, it is time to build the shed using our new tool. We should work through several examples to know how to apply the formula. Maybe later; I'm tired of typing for now!